Use case: Optimization

We are going to implement QAOA for the MaxCut problem

we start by importing qiskit to simulate circuits and some other basic libraries

import networkx as nx
import numpy as np
import pylab as pl
from mpl_toolkits.axes_grid1 import make_axes_locatable
from qiskit import *
from qiskit.visualization import *

networkx can be used to handle graphs

V = np.arange(0, 2, 1)
E = [(0, 1, 1.0)]

G = nx.Graph()
G.add_nodes_from(V)
G.add_weighted_edges_from(E)

nx.draw_networkx(G)
np.array(list(G.nodes)), V

(array([0, 1]), array([0, 1]))

We define a function that creates our circuit

def createCircuit(x, G, depth):
    V = list(G.nodes)
    num_V = len(V)
    q = QuantumRegister(num_V)
    c = ClassicalRegister(num_V)
    circ = QuantumCircuit(q, c)
    # uniform superposition
    circ.h(range(num_V))
    circ.barrier()
    for d in range(depth):
        gamma = x[2 * d]
        beta = x[2 * d + 1]
        # go through all edges and add Rzz gate
        for edge in G.edges():
            i = int(edge[0])
            j = int(edge[1])
            w = G[i][j]["weight"]
            circ.cx(q[i], q[j])
            circ.rz(w * gamma, q[j])
            circ.cx(q[i], q[j])
        circ.barrier()
        # add the mixer
        circ.rx(2 * beta, range(num_V))
        circ.barrier()
    circ.measure(q, c)
    return circ

draw example circuits

createCircuit(np.array((np.pi, np.pi)), G, 1).draw(output="mpl")

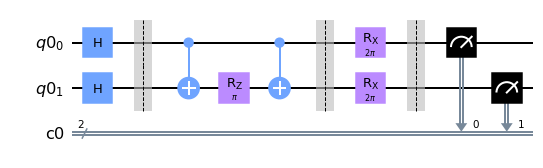
createCircuit(np.array((np.pi, np.pi, 1, 2)), G, 2).draw(output="mpl")

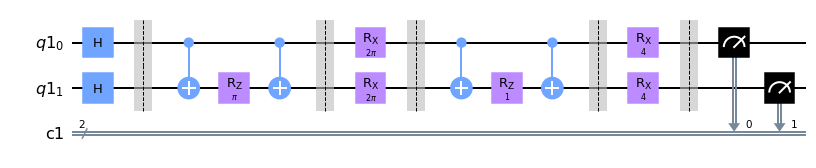
in order to evaluate a solution we define a function that gives us the cost

def cost(x, G):
    C = 0
    for edge in G.edges():
        i = int(edge[0])
        j = int(edge[1])
        w = G[i][j]["weight"]
        C = C + w / 2 * (1 - (2 * x[i] - 1) * (2 * x[j] - 1))
    return C

brute force function that lists all 2^n possibilities and finds the best solutions (use with caution)

def listcosts(G):
    costs = {}
    maximum = 0
    solutions = []
    V = list(G.nodes)
    num_V = len(V)
    for i in range(2**num_V):
        binstring = "{0:b}".format(i).zfill(num_V)
        y = [int(i) for i in binstring]
        costs[binstring] = cost(y, G)
        maximum = max(maximum, costs[binstring])
    for key in costs:
        if costs[key] == maximum:
            solutions.append(key)
    return costs, maximum, solutions

listcosts(G)

({'00': 0.0, '01': 1.0, '10': 1.0, '11': 0.0}, 1.0, ['01', '10'])

the result of a circuit contains a dictionary containing bitstrings together with how many times they have occured

we define a function that gives us (an approximation of) the expectationvalue based on this

def expectationValue(data, G):
    res = data.result().results
    E = []
    V = list(G.nodes)
    num_V = G.number_of_nodes()
    for result in res:
        n_shots = result.shots
        counts = result.data.counts
        e = 0
        for hexkey in list(counts.keys()):
            count = counts[hexkey]
            binstring = "{0:b}".format(int(hexkey, 0)).zfill(num_V)
            y = [int(i) for i in binstring]
            e += cost(y, G) * count / n_shots
        E.append(-e)
    return E

we will use an ideal simulator

ideal_sim = Aer.get_backend("qasm_simulator")

to get the energy/training/cost landscape for depth p=1, we sample the region \([0,\frac{\pi}{2}]^2\)

circuits = []
n = 16
for gamma in np.linspace(0, np.pi, n):
    for beta in np.linspace(0, np.pi, n):
        circuits.append(createCircuit(np.array((gamma, beta)), G, 1))

job_sim = execute(circuits, ideal_sim, shots=1024 * 2 * 2 * 2)

val = expectationValue(job_sim, G)
E = np.array(val).reshape(n, n)

f = pl.figure(figsize=(6, 6), dpi=80, facecolor="w", edgecolor="k")
_ = pl.xlabel(r"$\gamma$")
_ = pl.ylabel(r"$\beta$")
ax = pl.gca()
im = ax.imshow(E, interpolation="bicubic", origin="lower", extent=[0, np.pi, 0, np.pi])
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
_ = pl.colorbar(im, cax=cax)

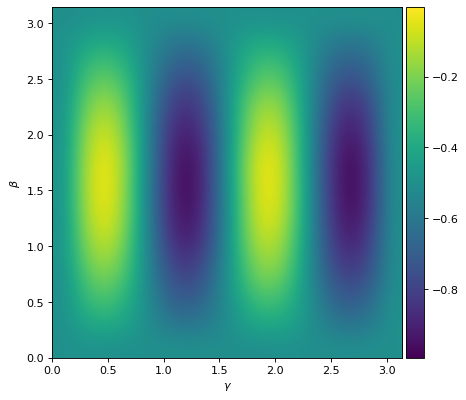
we import minimizers from scipy to do local minimization

from scipy import optimize as opt

the minimize funciton needs a function to evalution, which we create next

def getval(x, backend):
    circ = createCircuit(x, G, 1)
    tcirc = transpile(circ, backend)
    j = execute(tcirc, backend, shots=1024 * 2 * 2 * 2)
    val = expectationValue(j, G)
    return val[0]

out = opt.minimize(
    getval,
    x0=(1, 1),
    method="Nelder-Mead",
    args=(ideal_sim),
    options={"xatol": 1e-2, "fatol": 1e-2, "disp": True},
)

Optimization terminated successfully.
         Current function value: -1.000000
         Iterations: 18
         Function evaluations: 36

f = pl.figure(figsize=(6, 6), dpi=80, facecolor="w", edgecolor="k")
_ = pl.xlabel(r"$\beta$")
_ = pl.ylabel(r"$\gamma$")
ax = pl.gca()
im = ax.imshow(E, interpolation="bicubic", origin="lower", extent=[0, np.pi, 0, np.pi])
_ = pl.plot(out.x[1], out.x[0], "xr")
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
_ = pl.colorbar(im, cax=cax)

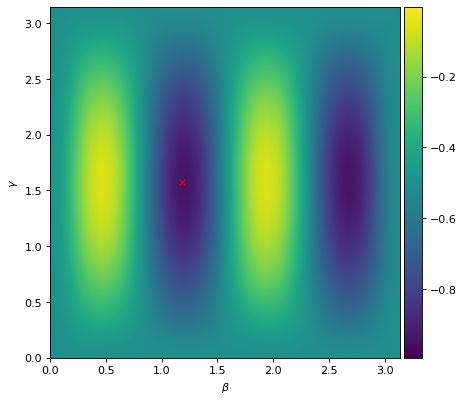
let’s plot the histogram

j = execute(createCircuit(out.x, G, 1), ideal_sim, shots=1024 * 2 * 2 * 2)

plot_histogram(j.result().get_counts())

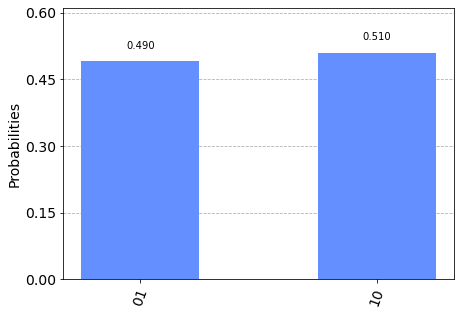
next, let’s see the effect of noise

we use a backend that emulates a real device “Vigo”

from qiskit.providers.aer import AerSimulator

from qiskit.test.mock import FakeVigo

device_backend = FakeVigo()
sim_vigo = AerSimulator.from_backend(device_backend)

plot_error_map(FakeVigo())

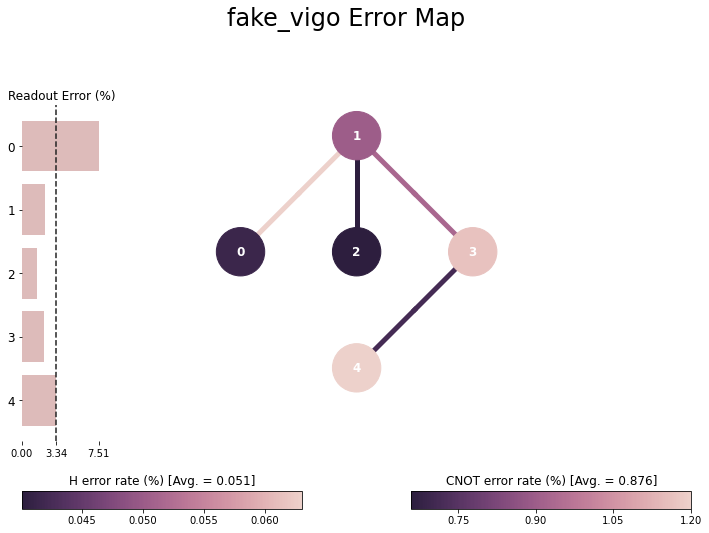
again, we sample the energy/training/cost landscape for depth p=1

noisy_circuits = []
n = 16
for gamma in np.linspace(0, np.pi, n):
    for beta in np.linspace(0, np.pi, n):
        circ = createCircuit(np.array((gamma, beta)), G, 1)
        # we need to transpile the circuit for the backend
        tcirc = transpile(circ, sim_vigo)
        noisy_circuits.append(tcirc)

job_sim_noise = execute(noisy_circuits, sim_vigo, shots=1024 * 2 * 2 * 2)

val_noise = expectationValue(job_sim_noise, G)
E_noise = np.array(val_noise).reshape(n, n)

we can now compare the landscape from the ideal and noisy simulation

(the circuit consist of only 2 qubits and 2 cnot gates)

f, axarr = pl.subplots(1, 2, figsize=(10, 10), dpi=80, facecolor="w", edgecolor="k")
vmin = min(np.min(E), np.min(E_noise))
vmax = min(np.max(E), np.max(E_noise))
_ = axarr[0].imshow(E, vmin=vmin, vmax=vmax, origin="lower", extent=[0, np.pi, 0, np.pi])
_ = axarr[1].imshow(
    E_noise, vmin=vmin, vmax=vmax, origin="lower", extent=[0, np.pi, 0, np.pi]
)
for i in range(2):
    _ = axarr[i].set_xlabel(r"$\beta$")
    _ = axarr[i].set_ylabel(r"$\gamma$")

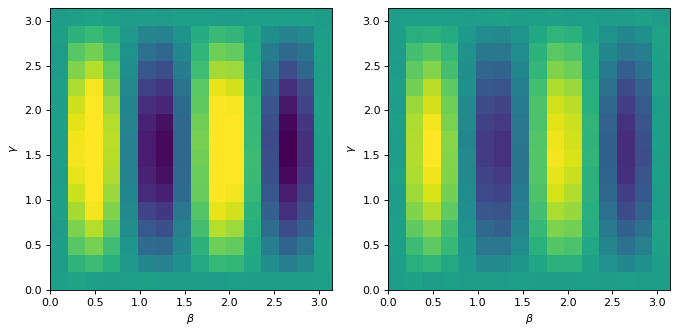
out_noise = opt.minimize(
    getval,
    x0=(1, 1),
    args=(sim_vigo),
    method="Nelder-Mead",
    options={"xatol": 1e-2, "fatol": 1e-2, "disp": True},
)

Optimization terminated successfully.
         Current function value: -0.894897
         Iterations: 20
         Function evaluations: 48

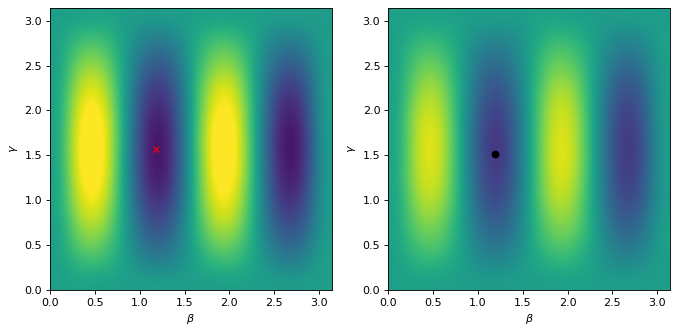
f, axarr = pl.subplots(1, 2, figsize=(10, 10), dpi=80, facecolor="w", edgecolor="k")
vmin = min(np.min(E), np.min(E_noise))
vmax = min(np.max(E), np.max(E_noise))
_ = axarr[0].imshow(
    E,
    vmin=vmin,
    vmax=vmax,
    origin="lower",
    extent=[0, np.pi, 0, np.pi],
    interpolation="bicubic",
)
_ = axarr[1].imshow(
    E_noise,
    vmin=vmin,
    vmax=vmax,
    origin="lower",
    extent=[0, np.pi, 0, np.pi],
    interpolation="bicubic",
)
_ = axarr[0].plot(out.x[1], out.x[0], "xr")
_ = axarr[1].plot(out_noise.x[1], out_noise.x[0], "ok")
for i in range(2):
    _ = axarr[i].set_xlabel(r"$\beta$")
    _ = axarr[i].set_ylabel(r"$\gamma$")

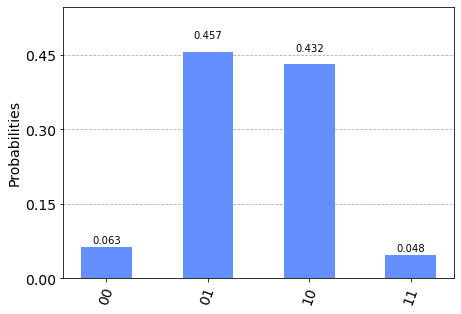
let’s plot the histogram. How did the noise effect it?

circ = createCircuit(out_noise.x, G, 1)
tcirc = transpile(circ, sim_vigo)
j = execute(tcirc, sim_vigo, shots=1024 * 2 * 2 * 2)

plot_histogram(j.result().get_counts())

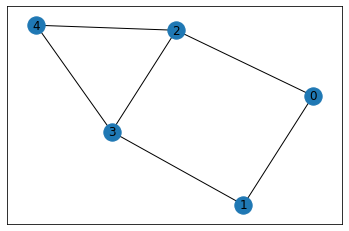
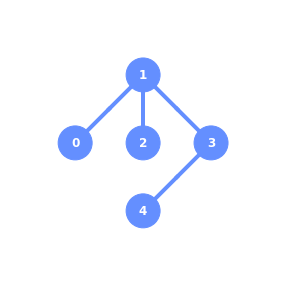
finally, let’s create a larger circuit

V = np.arange(0, 5, 1)
E = [(0, 1, 1.0), (0, 2, 1.0), (2, 3, 1.0), (3, 1, 1.0), (3, 4, 1.0), (4, 2, 1.0)]

G = nx.Graph()
G.add_nodes_from(V)
G.add_weighted_edges_from(E)

nx.draw_networkx(G)

what are the solutions?

l, m, maxcost = listcosts(G)
print(m, maxcost)

5.0 ['01100', '01101', '10010', '10011']

how does the circuit look?

createCircuit(np.array((0.4, 0.1)), G, 1).draw(output="mpl")

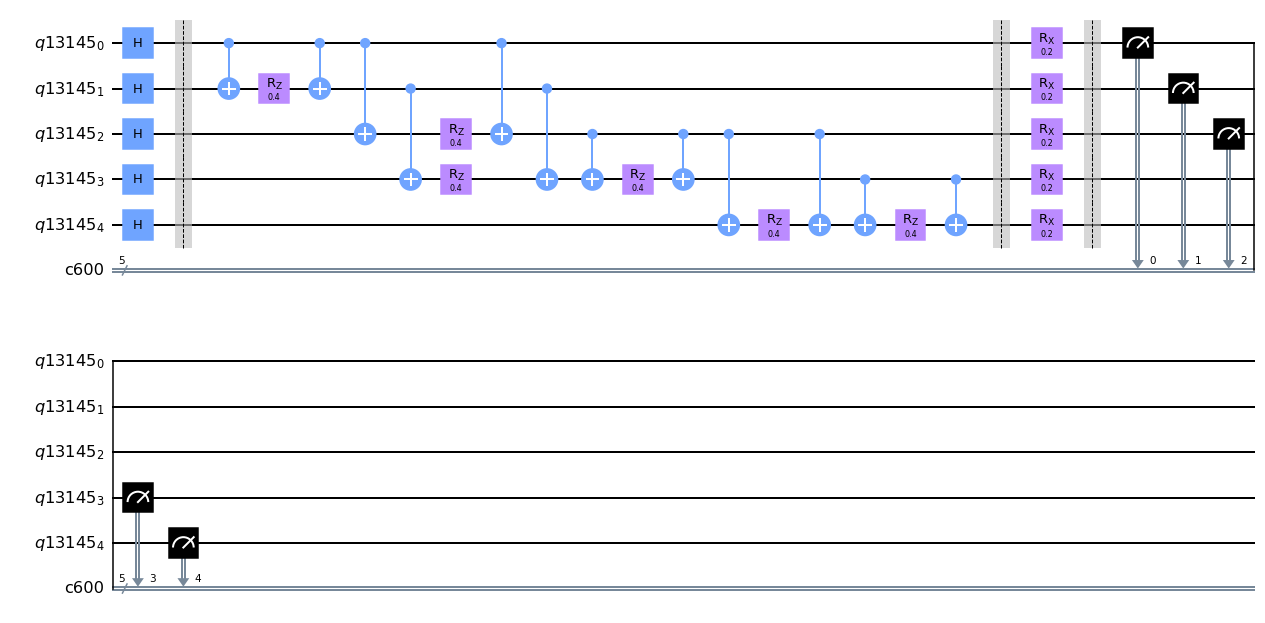
how does the circuit look on a real device?

plot_gate_map(FakeVigo())

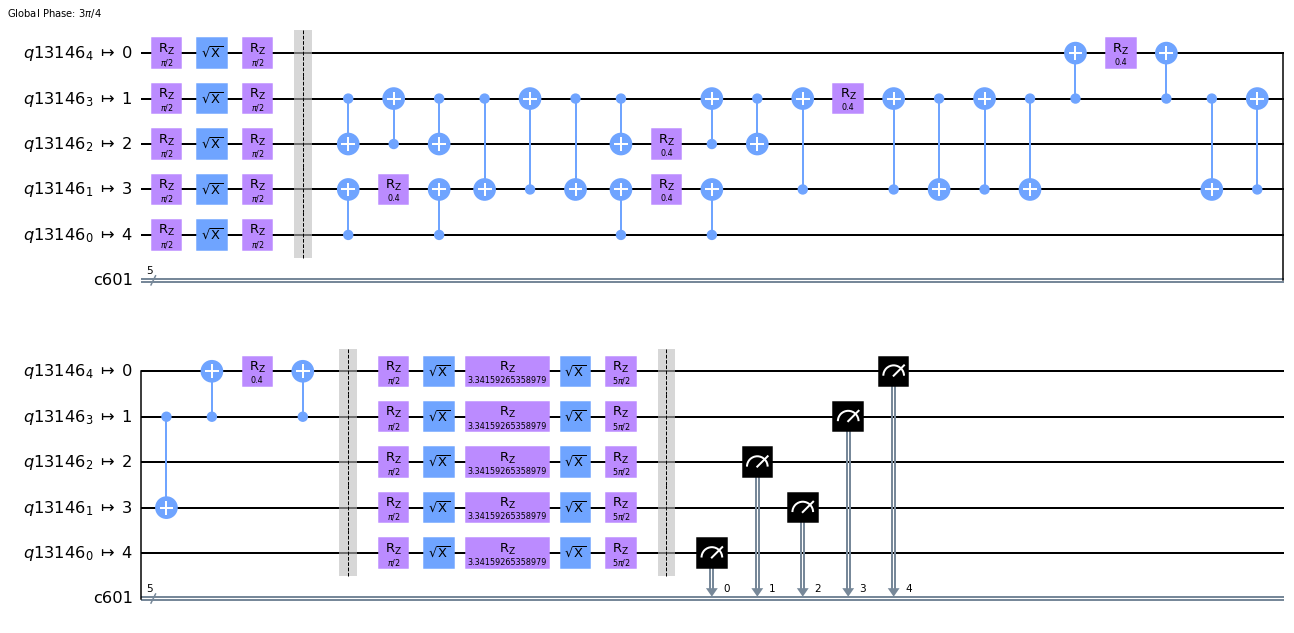
transpile(createCircuit(np.array((0.4, 0.1)), G, 1), backend=sim_vigo).draw(output="mpl")

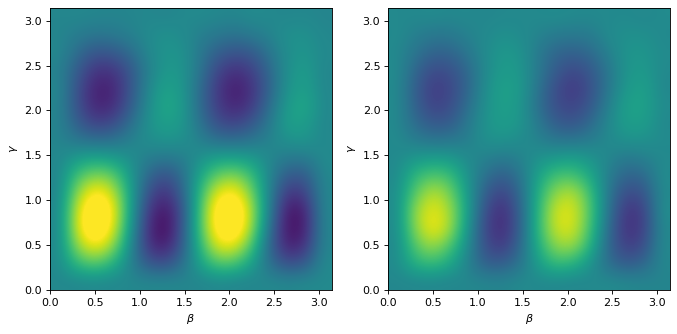
create energy landscapes for ideal and noisy simulations

circuits = []
n = 16
for gamma in np.linspace(0, np.pi, n):
    for beta in np.linspace(0, np.pi, n):
        circ = createCircuit(np.array((gamma, beta)), G, 1)
        circuits.append(circ)

job_sim = execute(circuits, ideal_sim, shots=1024 * 2 * 2 * 2)

val = expectationValue(job_sim, G)
E = np.array(val).reshape(n, n)

noisy_circuits = []
n = 16
for gamma in np.linspace(0, np.pi, n):
    for beta in np.linspace(0, np.pi, n):
        circ = createCircuit(np.array((gamma, beta)), G, 1)
        # we need to transpile the circuit for the backend
        tcirc = transpile(circ, sim_vigo)
        noisy_circuits.append(tcirc)

job_sim_noisy = execute(noisy_circuits, sim_vigo, shots=1024 * 2 * 2 * 2)

val_noisy = expectationValue(job_sim_noisy, G)
E_noise = np.array(val_noisy).reshape(n, n)

a comparison of the energy landscapes

f, axarr = pl.subplots(1, 2, figsize=(10, 10), dpi=80, facecolor="w", edgecolor="k")
vmin = min(np.min(E), np.min(E_noise))
vmax = min(np.max(E), np.max(E_noise))
_ = axarr[0].imshow(
    E,
    vmin=vmin,
    vmax=vmax,
    origin="lower",
    extent=[0, np.pi, 0, np.pi],
    interpolation="bicubic",
)
_ = axarr[1].imshow(
    E_noise,
    vmin=vmin,
    vmax=vmax,
    origin="lower",
    extent=[0, np.pi, 0, np.pi],
    interpolation="bicubic",
)
# _=axarr[0].plot(out.x[1],out.x[0],'xr')
# _=axarr[1].plot(out_noise.x[1],out_noise.x[0],'ok')
for i in range(2):
    _ = axarr[i].set_xlabel(r"$\beta$")
    _ = axarr[i].set_ylabel(r"$\gamma$")

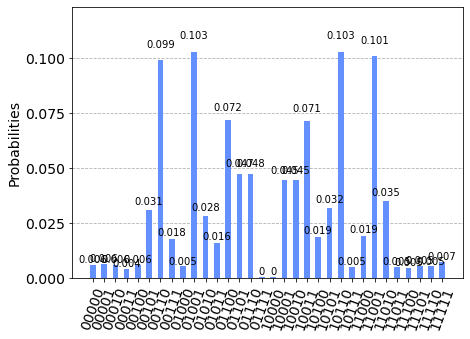
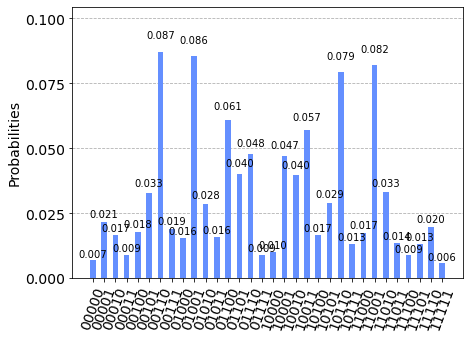
histograms of the best solution at depth p=1

out = opt.minimize(
    getval,
    x0=(1, 1),
    args=(ideal_sim),
    method="Nelder-Mead",
    options={"xatol": 1e-2, "fatol": 1e-2, "disp": True},
)
circ = createCircuit(out.x, G, 1)
j = execute(circ, ideal_sim, shots=1024 * 2 * 2 * 2)
plot_histogram(j.result().get_counts())

Optimization terminated successfully.
         Current function value: -3.890503
         Iterations: 14
         Function evaluations: 28

out_noise = opt.minimize(
    getval,
    x0=(1, 1),
    args=(sim_vigo),
    method="Nelder-Mead",
    options={"xatol": 1e-2, "fatol": 1e-2, "disp": True},
)
circ = createCircuit(out_noise.x, G, 1)
tcirc = transpile(circ, sim_vigo)
j = execute(tcirc, sim_vigo, shots=1024 * 2 * 2 * 2)
plot_histogram(j.result().get_counts())

Warning: Maximum number of function evaluations has been exceeded.

Where to go next? Try increasing the depth…